Graficación

 1er parcial

Evidencia realizada durante la clase

Ecuaciones matemáticas que representan las primitivas de la graficación

Puntos

Una gráfica de puntos es adecuada para representar datos cuantitativos o numericos se usan principalmente para comparar grupos de datos o distribuciones.

Un punto es creado por operadores and, or o not debido a que solo es necesario un pixel.

Líneas

Una línea es un conjunto de puntos alineados de forma recta entre ellos, sin embargo en la graficación estos se presentan en forma de escalera debido a los pixeles que necesitan.

 La ecuación para una línea es Y=mx+b donde m representa la pendiente.

Donde b es la intersección de Y y depende de las coordenadas dadas (X1,X2) y (Y1,Y2) . 

El algoritmo para la realización de una recta está dado por la ecuación inicial Y=mx+b y los cálculos de m=y2-y1 / X2-X1  y de  b= y1= m* X1

 Para el seguimiento de una línea se usa un algoritmo llamado DDA (digital diferencial analyzer)este es un método para calcular posiciones de pixeles,  este consiste en el rastreo de una línea aproximando los puntos a valores enteros cerca de la línea con las ecuaciones delta Y =m▲X y  ▲Y = ▲Y/m. a ecuación básica para el trazado de una línea es de la manera yk+1=Xk + 1/m  dependiendo si la pendiente es menor o igual a 1 puesto que el valor k va incrementando de unidad en unidad calculando el valor sucesivo.

 El algoritmo toma las posiciones del pixel en los extremos, las diferencias de x y Y entre las posiciones de los pixeles de los extremos dx y dy, al tener las posiciones del siguiente pixel se determina la trayectoria de la línea.

Circulos

Es una línea curvada con eje en el centro dividida en 8 secciones simétricas y todas estas equidistantes del punto céntrico.

Su ecuación esta definida por o   F(x,y)= X2+Y2 -r2

En donde cualquiera que sea el punto que se tome como parte de la circunferencia con un radio especifico cumple con la ecuación f(x,y)=0.

Sin embargo los puntos y el resultado que arroje la ecuación nos habla de donde esta posicionado de acuerdo a lo siguiente:

F(x , y)= 0 El punto se encuentra en la curva del circulo

F(x , y)> 0 El punto se encuentra encima de la curva

F(x , y)< 0 El punto se encuentra debajo de la curva

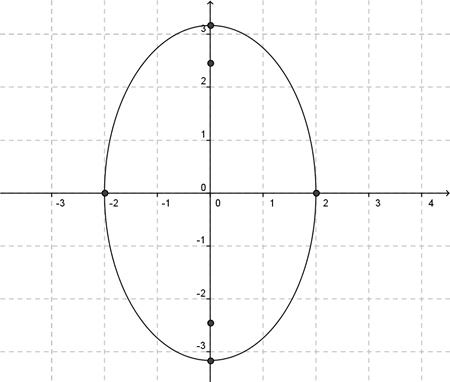
Elipses

Una elipse es una circunferencia alargada con 2 ejes perpendiculares llamados focos en donde la suma de las distancias entre un punto y los dos focos debe ser igual en todos los puntos.

Su ecuación general es d1+d2=k donde k representa una constante, donde d1 y d2 representan las distancias del punto hacia los focos.

Por lo tanto tenemos que la ecuación de una elipse esta dada por

Ax2+ Bx2+ CXy+Dx+Ey+E=0

Parábolas

Una parábola es un conjunto de puntos que están equidistantes de un foco y una directriz llamada "r" y donde el eje focal se llama vértice.

La ecuacion y = Ax^2 + Bx + C representa una parábola de forma vertical. En esta ecuación el termino "A" juega un papel importante en la orientación de la curva, puesto que si esta es positiva, la parábola es concava hacia arriba, si esta es negativa es concava hacia abajo, "B" representa la pendiente con respecto a su corte en Y, y  donde C es el punto del eje de las Y por el que pasa la parábola.

Hipérbola

Una hipérbola es un par de curvas planas y simetricas separadas pero a la vez dispuestas perpendicularmente entre sí, estas poseen un par de focos de los cuales su relación resulta ser una constante.
Se tiene que su ecuación | d(P,F)−d(P,F') | = 2⋅a donde se expresa la distancia de un punto genérico a los focos respectivos y donde 2⋅a representa una constante.

Para una hiperbola de eje focal horizontal (x−x0)2 / a2 − (y−y0)2 / b2 = 1. 
Y donde el eje focal es vertical es (y−y0)2 / a2 − (x−x0)2 / b2 = 1.
Y donde su eje focal horizontal esta centrada en el origen x2 / a2 − y2 / b2 = 1.
Eje focal vertical centrado en el origen y2 / a2 − x2 / b2 = 1 donde a representa el eje real y b el eje imaginario.

Curvas

Una curva es una línea que se desvía de la dirección recta sin formar ángulos. Esto quiere decir que su dirección varía de manera paulatina y constante. Para conocer la ecuación de una curva necesitamos conocer los puntos donde ésta intercepta al eje x, conocidos como raíces.

ECUACIÓN DE LA CURVA AX2+BX+C=0

Estas curvas cortan al eje x en dos puntos; éstos nos ayudarán a encontrar la ecuación de la curva. Asumamos que la curva ax2+bx+c=0 corta al eje x en los puntos (α,0) y (β,0). Entonces la ecuación de la curva será:

X2 – (Α + Β)X + ΑΒ = 0

ECUACIÓN DE LA CURVA AX3+BX2+CX+D= 0

Estas curvas cortan al eje x en tres puntos; éstos nos ayudarán a encontrar la ecuación de la curva. Asumamos que la curva ax3+bx2+cx+d=0 corta al eje x en los puntos (α,0), (β,0) y (γ,0). Entonces la ecuación de la curva será:

X3 – (Α + Β + Γ) X2 + (ΑΒ + ΒΓ + ΑΓ) X – ΑΒΓ=0

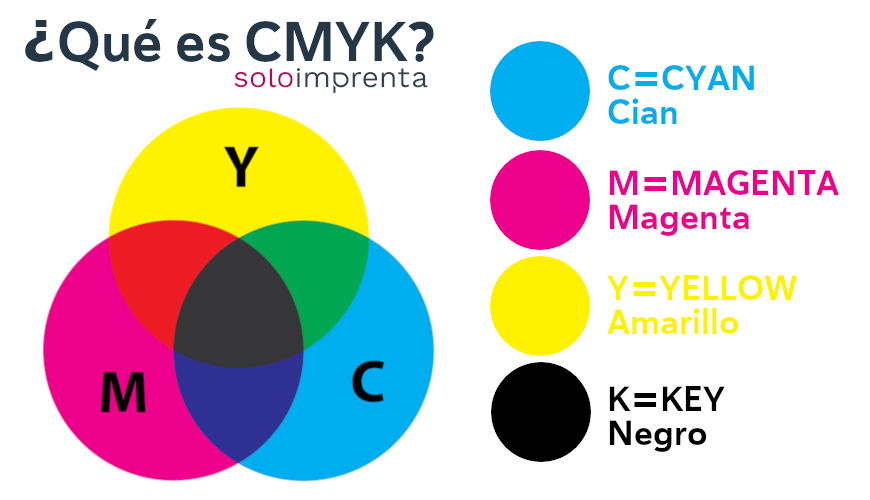
Modelos de color

Modelo HSV:

Sus siglas significan (Hue Saturation Value) que en español seria Matiz, Saturación y Valor.
Es una de las representaciones más fieles a la forma en que los humanos percibimos los colores.
Este modelo es bastante usado en las aplicaciones gráficas o en sus interfaces para que el usuario pueda elegir colores y al mismo tiempo sus grados de saturación y el brillo del mismo.
Un ejemplo de este modelo de color sería en el color rojo que sería:

 H = 0, S = 100, V = 100

Modelo RGB

Este modelo de colores están compuestos por los colores rojo, verde y azul (del ingles red, green and blue),este modelo de color es uno de los más basicos ya que la mayor parte de los colores secundarios parten desde este modelo, mismo que se han ocupado en muchas areas de aplicacion, están sobretodo en el area de la electronica, tales como la resolucion grafica de las televisiones, hay luces LEDS que tambien los determina, los telefonos tambien se comportan al igual que en la television en cuestion de la mezcla de colores.

modelo CMYK

los colores que los destaca son Cyan, Magenta, Amarillo y Negro. Este modelo destaca para tener imagenes de impresiones con tinte, van complementados con los colores RGB, sin embargo, solamente es una parte que se distingue, lo que es la sensacion de manejarlo en el diseño grafico, ya que se ocupa de una luminosidad para definir los colores.

Modelo HSL

Se representa con 3 tonalidades, que son:
Matiz, Saturación y luminosidad, comúnmente se utiliza este modelo para la creación de imágenes digitales, a diferencia del modelo HSV, podemos aplicar una iluminación que no pueda tender mucho a blanco, sino que pueda llegar a una tonalidad grisacea ,éste nos permite fijar la saturación entre gris y color puro para los colores como rojo,  amarillo, verde, cian, azul, entre otros colores. Respecto al matiz, nos permite virar los colores a los adyacentes, por ejemplo, para el rojo, desde magenta a naranja o de verde a azul.